Dragons are mythical creatures, but we can use them as a tool to learn Mendelian inheritance. Here you will find assumptions that we made about genetics, phenotypes and breeding of dragons.
Chromosomes
Every dragon has 14 chromosomes. It is a diploid , which means it has two sets (or pairs) of 7 chromosomes (2 x 7 = 14). Each set comes from one parent.
The image below shows a simplified representation of chromosomes of a randomly simulated dragon.
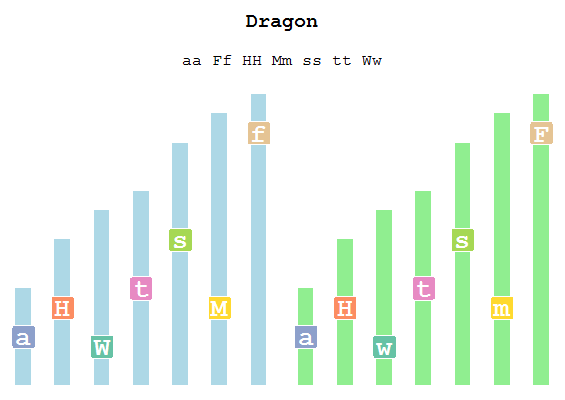
We can see that one set of 7 chromosomes is colored in blue, whereas the second set is colored in green. We can assume that the blue set comes from the dragon’s father, whereas the green one from its mother.
In nature, each chromosome carries information about many genes. In our simulation, we are investigating only one gene on each of the chromosome pairs.
Humans are also diploid. If you wanted to compare dragons to humans, humans have 46 chromosomes, sorted into 23 pairs. One chromosome in each of the 23 pairs is from the person’s father, the other from their mother.
Reproduction
Once a dragon becomes a parent and passes its genes to the offspring, it produces a gamete containing 7 chromosomes. This gamete contains a randomly selected chromosome from each pair, so it usually will be a mix of chromosomes, like this:
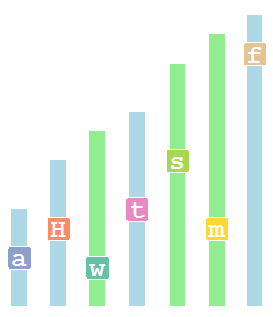
It might happen that a gamete will contain all chromosomes that originally came from one parent of the dragon (i.e. all blue or all green chromosomes). However, taking into account all the possible combinations, it is just less probable.
Genes and alleles
We are investigating seven different dragon traits (e.g. the ability to breathe fire), and each of them is controlled by a single gene – we say that such a trait is monogenic.
It is believed that facial dimples are an example of human monogenic trait.
As each dragon has two sets of chromosomes, it can have two versions of each gene. Different alleles for a gene are often denoted with different versions of the same letter.
For example, you might see a dragon with “A” and “a” alleles of the gene encoding body and head color (let’s call it the BH gene). One allele is written in uppercase – “A”, the other in lowercase – “a”.
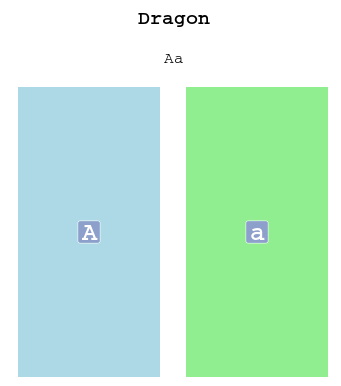
This dragon would be called a heterozygote with respect to the BH gene. We could also say that it has “Aa” genotype.
Of course, there are also two other options of genotype that dragons could have (for the BH gene): the “AA” and “aa” genotype.
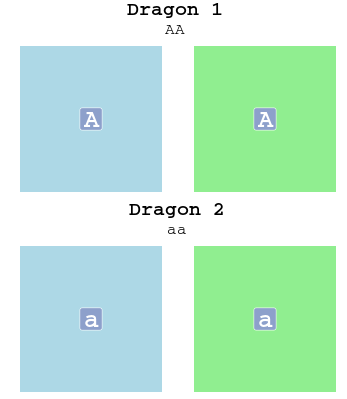
These two dragons would be called homozygotes with respect to the BH gene.
A dragon can be a homozygote for one gene, but a heterozygote for the other (ex. a dragon with the “AA Tt” genotype)
In nature, many different forms (alleles) may exist for any gene, but each diploid organism can have a maximum of only two alleles (one from each of the parents). The two copies of the gene that an organism has may be the same or different alleles.
Phenotypic traits
Our dragons can have 7 monogenic traits, and each gene has two versions. But how a dragon’s genotype (information that is stored in genes) translates to its phenotype (the observable traits)?
Well, the simulation assumes that each gene has two alleles: one dominant and one recessive. The dominant alleles are those written in uppercase (ex. “A”), whereas the recessive are written in lowercase (ex. “a”).
Going back to our example:
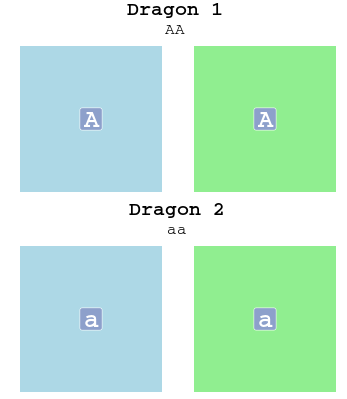
The first dragon has two dominant alleles (“AA”), while the second dragon has two recessive alleles (“aa”). As you can read from the phenotype table, the first dragon will have blue body and head, and the second – green body and head.
But what happens, when a dragon is a heterozygote (i.e. “Aa”)?
If one dominant allele (upper-case letter) is present, the dominant trait will occur (e.g. the dragon will have blue body and head). The recessive trait (e.g. the green body and head) will only occur if the dragon has two copies of the recessive allele. So, our heterozygote “Aa” dragon will have blue body and head. The recessive allele is masked by the presence of the dominant one.
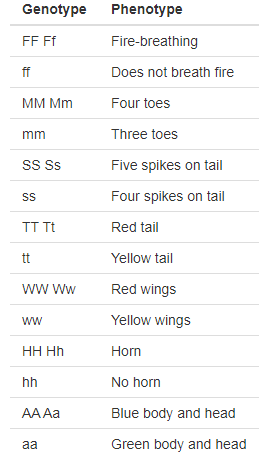
Phenotype table
The following tables show the traits (phenotype) that a dragon might have, depending on its genetic information (genotype).
Exercises

